hvad er en ligedannet trekant
Egenskaber ved en ligedannet trekant
Som nævnt er en ligedannet trekant defineret som en trekant, hvor alle sider er lige store, og alle vinkler er lige store. Det betyder, at en ligedannet trekant har tre lige store indre vinkler, som hver måler 60 grader.
I en ligedannet trekant er de modstående sider parallelle, og de modstående vinkler er også lige store. Derudover, hvis en trekant er ligedannet, er den også ligebenet.
Regneformler for ligedannede trekanter
Regneformlerne for ligedannede trekanter er vigtige at kende, da de kan anvendes til at beregne sidelængder og vinkler i en given trekant. Hvis to trekanter er ligedannede, kan forholdet mellem de tilsvarende sider i de to trekanter findes ved hjælp af en enkel formel:
a/a’ = b/b’ = c/c’,
hvor a, b og c er sidelængderne i den ene trekant, og a’, b’ og c’ er sidelængderne i den anden trekant.
Ved hjælp af denne formel kan man finde en manglende sidelængde, hvis man kender forholdet mellem sidelængderne i to ligedannede trekanter. For eksempel, hvis man kender to sidelængder i en trekant og forholdet mellem de to sider i en ligedannet trekant, kan man beregne den manglende sidelængde.
Bevis for ligedannede trekanter
Et bevis for ligedannede trekanter kan gøres ved at vise, at de tre vinkler og de tre sider er ens i de to trekanter. Hvis to trekanter har ens vinkler, men de ikke er ligedannede, kan det bevises, at sidelængderne i de to trekanter ikke er ens.
Anvendelser af ligedannede trekanter i geometrien
Ligedannede trekanter er vigtige i geometrien, da de kan bruges til at beregne sidelængder og vinkler i en trekant og i andre former af polygoner. De kan også bruges til at beskrive forholdet mellem to polygoner, hvis de er ligedannede.
Eksempler på hverdagsanvendelser af ligedannede trekanter
Ligedannede trekanter findes også i hverdagen. Et eksempel på en hverdagsanvendelse af ligedannede trekanter er, når man køber billegetøj. Billegetøjet er ofte bygget med ligedannede trekanter for at spare materialer og samtidig opnå den samme form og størrelse.
Ligedannede trekanter i pythagoræisk tripler
En pythagoræisk trippel er en gruppe af tre positive hele tal a, b og c, hvor a^2 + b^2 = c^2. Ligedannede trekanter indgår ofte i pythagoræiske tripler, da en retvinklet trekant kan opdeles i to sådanne trekanter.
Undervisning i ligedannede trekanter i folkeskolen og gymnasiet
I folkeskolen og gymnasiet undervises elever i geometri, inklusive om ligedannede trekanter. Elever lærer, at en ligedannet trekant har lige store sider og lige store vinkler og at de tre lige store vinkler i en ligedannet trekant hver måler 60 grader.
FAQs
Hvor mange grader er der i en trekant?
I en trekant er der altid 180 grader.
Hvordan beregner man arealet af en trekant?
Arealet af en trekant kan beregnes ved at gange halvdelen af basen (grunden) med højden. A = 1/2bh.
Hvordan beregner man siderne i en trekant?
For at beregne sidelængderne i en trekant kan man anvende Pythagoras’ sætning eller trigonometriske formler.
Hvordan beregner man sidelængden i en retvinklet trekant?
I en retvinklet trekant, kan sidelængden beregnes ved at anvende Pythagoras’ sætning, som siger, at a^2 + b^2 = c^2, hvor c er hypotenusen, og a og b er kateterne.
Hvordan finder man vinklerne i en retvinklet trekant?
I en retvinklet trekant er vinklen modsat hypotenusen altid 90 grader. De to andre vinkler kan findes ved at anvende trigonometriske funktioner, som sinus, cosinus og tangent.
Hvordan beregner man en retvinklet trekant?
En retvinklet trekant kan beregnes ved at kende to sidelængder, eller en sidelængde og en vinkel.
Hvad er sinus, cosinus og tangent?
Sinus, cosinus og tangent er trigonometriske funktioner, som bruges til at finde sidelængder og vinkler i en trekant.
Hvad er en stumpvinklet trekant?
En stumpvinklet trekant er en trekant, hvor en af vinklerne er større end 90 grader.
Keywords searched by users: hvad er en ligedannet trekant hvor mange grader er der i en trekant, areal af trekant, beregn sider i trekant, beregn sidelængde i retvinklet trekant, vinkler i en retvinklet trekant, beregn retvinklet trekant, hvad er sinus, stumpvinklet trekant
Categories: Top 24 hvad er en ligedannet trekant
Ligedannede trekanter
Hvordan regner man ligedannede trekanter?
Hvad er en ligedannet trekant?
En ligedannet trekant er en trekant, hvor alle tre vinkler er parvis ens, og alle tre sider har samme proportionelle dimensioner. Med andre ord vil en ligedannet trekant altid have samme form som en anden, uanset størrelse og roteringsvinkel.
De fleste ligedannede trekanter er retvinklede, hvilket betyder, at den største vinkel i trekanten er en ret vinkel på 90 grader. Men de kan også være skæve, hvor den største vinkel er mindre end 90 grader, eller obtus, hvor vinklen er større end 90 grader.
Hvordan regner man ligedannede trekanter?
For at beregne en ligedannet trekant skal du normalt kun kende dimensionerne i én trekant – for eksempel de tre sidelængder eller en sidelængde og en vinkel, og så kan du bruge proportioner til at beregne de manglende dimensioner. Proportionerne siger, at for holdene mellem siderne i en ligedannet trekant, er de samme forholdsværdier i begge trekanter.
For eksempel, lad os sige, at vi har en ligedannet trekant med siderne 4, 8 og 10 cm. Nu vil vi finde ud af størrelsen af en anden trekant, som har en hypothenuse på 20 cm og en af de andre sider har længden 5 cm. Vi ved allerede, at de to trekanter er ligedannede, da de har de samme vinkler, og nu skal vi bare finde ud af forholdet mellem de to søgeværdier.
Hvis vi kalder a og b som de to sider af den første trekant med en hypotenuse på 10, og vi kalder m og n for de to søgesider med hypotenuser på 20 og 5, så kan vi definere en proportional ligning, der siger:
a:b = m:n, da de to trekanter er ligedannede.
Vi ved allerede, at siden med længden 10 er proportional med hypotenusen med længden 20, og nu vil vi finde forholdet mellem siden med længden 4 og siden med længden 8 i den oprindelige trekant, til den søgte side med længden 5 i den anden trekant. Her er formelen som følger:
4/8 = 5/x,
Hvor x er længden af den tredje side i den anden trekant. Nu kan vi løse for x ved først at multiplicere begge sider med 8 for at få:
4 × (5/8) = x,
x = 2,5.
Så den anden trekant har dimensionerne 5, 10 og 2,5 cm.
Hvordan kan man anvende ligedannede trekanter?
Ligedannede trekanter kan have mange anvendelser i den virkelige verden. For eksempel kan vi anvende dem til at måle højder på objekter, eller til at beregne afstande til fjerntliggende objekter, såsom træer eller huse. Vi kan også bruge dem til at beregne størrelsen af objekter, som vi ellers ikke ville kunne måle direkte, såsom Planck-længden i kvantemekanikken.
En af de mest almindelige anvendelser af ligedannede trekanter er på felter som arkitektur og ingeniørvidenskab, hvor det er nødvendigt at beregne dimensionerne og afstandene i bygninger og strukturer. For eksempel kan ingeniører bruge ligedannede trekanter til at beregne afstanden mellem to fjernsynstårne ved at måle højden og vinklen fra et bestemt punkt på jorden.
I geometrien kan ligedannede trekanter også bruges til at bevise matematiske teoremer og formler. For eksempel kan vi bevise, at to parallelle linjer skåret af en tredje linje danner en matchvinkel ved hjælp af proportionaliteten mellem ligedannede trekanter.
FAQs
1. Hvordan kan jeg identificere en ligedannet trekant i praksis?
En ligedannet trekant vil som regel have nogle identificerbare træk. For eksempel vil alle tre vinkler være ens, og alle tre sider vil have samme proportionelle dimensioner. Hvis du har kendskab til dimensionerne i en enkelt trekant, kan du bruge proportioner til at se, om de er ligedannede.
2. Kan jeg bruge ligedannede trekanter til at beregne dimensionerne i cirkler og sfærer?
Ja, ligedannede trekanter kan anvendes til at beregne dimensionerne i en lang række geometrisk figurer, herunder cirkler og sfærer. I disse tilfælde kaldes det ofte at bruge trigonometriske formler og teoremer.
3. Hvordan kan ligedannede trekanter hjælpe mig med at beregne afstanden mellem to genstande?
Hvis du kender en bestemt dimension, som for eksempel højden på en person eller træ, kan du bruge en ligedannet trekant til at beregne afstanden til personen eller træet. Du skal bare bruge en måleinstrument og proportionalitetsformlen for at beregne afstanden.
Konklusion
Ligedannede trekanter er en vigtig del af geometrien og er grundlaget for mange matematiske og praktiske beregninger. Ved at forstå proportioner og ligedannede trekanter, kan du beregne dimensioner og afstande i bygninger, maskiner og andre fysiske opgaver, som det er vigtigt at have præcise målinger på. Hvis du vil lære mere om geometriske figurer og proportioner, kan du anvende online ressourcer og tutorials eller konsultere en matematiklærer eller et videnskabeligt geni for at få hjælp.
Hvad er formlen for en ligebenet trekant?
En formel er en matematisk udtryk, der beskriver sammenhængen mellem to eller flere variable. Formlen for en ligebenet trekant indeholder normalt længderne af de to lige lange sider, samt længden af den tredje side og vinklen mellem de to lige lange sider. Denne formel kan bruges til at beregne forskellige egenskaber af trekanten, såsom omkredsen, arealet og vinklerne.
Formlen for en ligebenet trekant er følgende:
a² + b² = c²
hvor a og b er længderne af de to lige lange sider, og c er længden af den tredje side, også kendt som hypotenusen. Hvis man kender længderne af a og b, kan man således beregne længden af c ved at tage kvadratroden af summen af a og b i kvadrat.
For eksempel, hvis to sider i en trekant er henholdsvis 3 cm og 3 cm, kan hypotenusen beregnes som følger:
c² = 3² + 3²
c² = 18
c = √18
c ≈ 4.24 cm
Nu hvor vi kender længderne af alle tre sider i trekanten, kan vi også beregne dens omkreds og areal. Omkredsen er simpelthen summen af længderne af alle tre sider, og arealet kan beregnes ved hjælp af den grundlæggende formel for trekantens areal, nemlig:
A = ½ * b * h
hvor b er basen af trekanten, og h er dens højde. I en ligebenet trekant med lige lange sider, vil basen og højden normalt være forskellige. I stedet bruger man ofte halvdelen af hypotenusen som basen, og højden som den del af den anden katete, der står vinkelret på hypotenusen. Således bliver arealet af en ligebenet trekant:
A = ½ * a * h
hvor h nu er højden, der står vinkelret på basen a. Hvis vi kender længderne af a og h, kan vi således finde arealet ved at sætte tallet ind i formlen og foretage en simpel udregning.
Et eksempel på en sådan beregning kunne være følgende: Hvis længden af den ene katete i en trekant er 4 cm, og højden fra denne katete til hypotenusen er 3 cm, kan arealet af trekanten beregnes som:
A = ½ * 4 * 3
A = 6 kvadratcentimeter
FAQs
Q: Kan en trekant være både ligebenet og ligesidet?
A: Ja, det kan den. En trekant kan være ligebenet og samtidig have lige lange sider. En sådan trekant kaldes en ligebenet og ligesidet trekant.
Q: Hvad er vinklerne i en ligebenet trekant?
A: De vinkler i en ligebenet trekant, der støder op til de lige lange sider, kaldes de to ligevinkler, og de er begge lige store. Den tredje vinkel, der ligger over for hypotenusen, er normalt forskellig fra de to ligevinkler og kan variere i størrelse afhængigt af størrelsen af de to lige lange sider.
Q: Er der andre formler, der kan bruges til at beregne egenskaber af en ligebenet trekant?
A: Ja, der er en række andre formler, der kan bruges til at beregne egenskaber af en ligebenet trekant. For eksempel kan man bruge sin, cos og tan funktionerne til at beregne vinkler og længder af andre sider, hvis man kender længderne af to af siderne og en af de vinkler, som de støder op til.
Q: Er der nogen praktiske anvendelser af en ligebenet trekant?
A: Ja, der er flere praktiske anvendelser af en ligebenet trekant. En af de mest almindelige anvendelser er til beregning af tagkonstruktioner, hvor ligebenet trekant er en almindelig form. Ligebenet trekant kan også anvendes til at beregne afstanden mellem to punkter, hvis man kender længden af en af de lige lange sider og vinklen mellem den side og en linje, der går gennem de to punkter.
I alt kan man sige, at formelen for en ligebenet trekant er en af de mest grundlæggende matematiske formler, og den er brugbar i mange sammenhænge, både i matematik og i den praktiske verden. Ved at forstå denne formel kan man ikke blot beregne egenskaber af en ligebenet trekant, men også anvende den til at løse en bred vifte af problemer og opgaver i mange fag.
See more here: thichvaobep.com
hvor mange grader er der i en trekant
En af de mest almindelige spørgsmål, der stilles af mange studerende eller mennesker interesseret i matematik, er hvor mange grader der er i en trekant. Svaret på dette spørgsmål afhænger af forskellige faktorer, især trekantens type og størrelse. Vi vil dykke dybt ind i dette emne i denne artikel og forsøge at besvare nogle af de mest almindelige spørgsmål, der er relateret til trekantens vinkler og grader.
Typer af trekanter
Før vi kan besvare spørgsmålet om trekantens vinkler og grader, er det vigtigt at kende de forskellige typer af trekanter. Der er tre grundlæggende typer af trekanter: lige linje (eller retvinklet), skarp (eller akut), og stump (eller obtus). Disse tre typer klassificeres efter deres indre vinkler og forholdet mellem deres linjesegmenter.
En lige linjetrekant har en ret vinkel, der måler 90 grader. Det betyder, at en af trekantens vinkler er lige, mens de to andre er skarpe. Højde og base i en lige linjetrekant danner ofte et rektangel, hvilket gør det lettere at beregne vinkler og grader.
En skarp trekant har tre skarpe vinkler, der hver måler mindre end 90 grader. En af de mest almindelige eksempler på en skarp trekant er en 30-60-90 trekant, hvor de tre vinkler måler henholdsvis 30, 60 og 90 grader.
En stump trekant har en stump vinkel, der måler mere end 90 grader. De to andre vinkler kaldes skarpe, da de hver måler mindre end 90 grader. En simpel måde at visualisere en stump trekant på er at forestille sig en trekant med en base, der er meget længere end dens højde.
Trekantens grader
Nu hvor vi kender trekantens typer, kan vi begynde at give svar på, hvor mange grader der er i en trekant.
Enhver trekant har tre vinkler, og summen af disse vinkler skal altid være lig med 180 grader. Dette er en grundlæggende egenskab ved en trekant og kan bevise ved hjælp af Euklids femte postulat, som siger, at hvis en linje skærer to parallelle linjer, skærer den også ind i to vinkler på hver side af linjen, hvis sum er 180 grader.
Dette betyder, at uanset hvilken type trekant vi har, er summen af alle dens vinkler altid 180 grader. Dette kan være nyttigt, når man skal beregne en manglende vinkel i en trekant.
For eksempel, hvis vi har en lige linjetrekant, og vi kender to af dens vinkler, kan vi nemt finde den tredje vinkel ved at subtrahere summen af de to kendte vinkler fra 180 grader. Hvis vi har en skarp trekant, og vi kender en af dens vinkler, kan vi også finde de to andre vinkler ved at følge samme logik.
Beregningsmetoder
Der er flere forskellige beregningsmetoder, der kan bruges til at finde vinkler og grader i en trekant. En af de mest anvendte metoder er trigonometri, som bruger sines, cosines og tangenter til at beregne vinkler og sider i en trekant.
I en trekant kan trigonometrien anvendes til at beregne forholdet mellem dens sider og dens vinkler. For eksempel kan vi bruge sine-funktionen til at beregne en given vinkel, hvis vi kender forholdet mellem en vinkel og den modsatte side af trekanten.
En anden metode, der kan bruges til at beregne vinkler og grader i en trekant, er den pythagoreiske teorem, som siger, at i en lige linjetrekant er summen af kvadraterne på de to korte sider (højde og base) lig med kvadratet på den lange side (hypotenusen). Denne metode kan være nyttig, når man skal beregne en ukendt vinkel eller længde i en lige linjetrekant.
FAQs
1. Hvordan finder jeg vinklerne i en trekant?
For at finde vinklerne i en trekant skal du kende mindst to af dens vinkler eller sider. Hvis du kender to vinkler, kan du finde den tredje vinkel ved at subtrahere summen af de to kendte vinkler fra 180 grader. Hvis du kender to sider og en vinkel i trekanten, kan du bruge trigonometri til at finde den manglende vinkel.
2. Hvordan beregner jeg arealet af en trekant?
For at beregne arealet af en trekant skal du kende dens højde og base. Arealet af en trekant beregnes ved at multiplicere højden med basen og dividere dette produkt med to. Formlen er A = (h x b) / 2.
3. Hvorfor er summen af vinklerne i en trekant altid 180 grader?
Summen af vinklerne i en trekant er altid 180 grader på grund af Euklids femte postulat, som siger, at hvis en linje skærer to parallelle linjer, skærer den også ind i to vinkler på hver side af linjen, hvis sum er 180 grader.
4. Hvilken type trekant har en ret vinkel?
En trekant med en ret vinkel kaldes en lige linjetrekant eller retvinklet trekant.
5. Hvordan kan jeg fortælle forskellen mellem en skarp og en stump trekant?
En skarp trekant har tre skarpe vinkler, der hver måler mindre end 90 grader, mens en stump trekant har en stump vinkel, der måler mere end 90 grader.
areal af trekant
En trekant er en geometrisk figur med tre sider og tre vinkler. Den kan have forskellige former og størrelser, men har altid de samme grundlæggende egenskaber. Enhver trekant har en højde, som er en linje, der går fra en af dens hjørner og står vinkelret på den modsatte side. Højden deler trekanten i to “halvdele”, og arealet af trekanten er derfor lig med halvdelen af produktet af højden og bredden af trekanten.
For at bruge denne formel til beregning af areal af en trekant har man brug for at kende hjælpeværdierne – højden og bredden af trekanten. Disse kan opnås ved hjælp af forskellige metoder, afhængigt af opgaven.
En simpel måde at finde højden af en trekant på er ved at tegne en linje fra hjørnet på den modsatte side, der er vinkelret på den side, som man vil finde højden for. Dette vil dele trekanten i to mindre trekanter, hvoraf den ene vil være en retvinklet trekant. Højden vil i dette tilfælde være den ene katete i den retvinklede trekant.
For at bestemme bredden af trekanten kan man måle længden af den basislinje, som trekanter er bygget op af. Hvis bredden ikke er kendt, kan det også være muligt at beregne det ved hjælp af trigonometriske funktioner og kendte vinkler.
En mere kompleks type af trekant kaldes for “areal af en retvinklet trekant”. En retvinklet trekant er kendetegnet ved én vinkel, som er præcis 90 grader (“ret”), og to andre vinkler, som tilsammen giver 90 grader. For at beregne arealet af en retvinklet trekant kan man bruge formlen halvdelen af produktet af længden af begge katete – også kendt som Pythagoras’ sætning.
Et andet eksempel på en trekantstype er en “ligebenet trekant”. Lige benede trekanter har to sider, der er lige lange, og den tredje side, der har en anden længde. For at finde arealet af en lige benet trekant, kan man beregne halvdelen af præsissen af de to lige sider og derefter anvende den tidligere nævnte formel.
En tredje type af trekant er “likesidede trekant”, som har alle sider lig med hinanden og vinkler på 60 grader. For at beregne arealet af en likesidet trekant kan man bruge formlen halvdelen af produktet af siden og længden af højden.
Frequently Asked Questions (FAQs)
Q: Hvorfor er areal af en trekant vigtig?
A: Areal af en trekant er en grundlæggende egenskab ved geometriske figurer og er vigtig i mange matematiske og scientiske sammenhænge. For eksempel kan det være nødvendigt at kende areal af en trekant for at bestemme parametre såsom volumen, hastighed eller vægt.
Q: Hvad er formlen for at beregne arealet af en trekant?
A: Arealet af en trekant er lig med halvdelen af produktet af højden og bredden af trekanten.
Q: Hvordan finder man højden af en trekant?
A: Højden af en trekant kan findes ved at tegne en linje fra hjørnet på den modsatte side, der er vinkelret på den side, som man vil finde højden for.
Q: Hvordan finder man bredden af en trekant?
A: Bredden af en trekant kan findes ved at måle længden af den basislinje, som trekanten er bygget op af.
Q: Hvad er en retvinklet trekant?
A: En retvinklet trekant er en type af trekant, der har én vinkel, der er præcis 90 grader (“ret”), og to andre vinkler, som tilsammen giver 90 grader.
Q: Hvordan beregner man arealet af en retvinklet trekant?
A: Arealet af en retvinklet trekant kan beregnes ved at anvende formlen halvdelen af produktet af længden af begge katete – også kendt som Pythagoras’ sætning.
Q: Hvad er en lige benet trekant?
A: En lige benet trekant er en type af trekant, hvor to sider er lige lange og den tredje side har en anden længde.
Q: Hvordan beregner man arealet af en lige benet trekant?
A: Arealet af en lige benet trekant kan beregnes ved at finde halvdelen af præsissen af de to lige sider og anvende den tidligere nævnte formel.
Q: Hvad er en likesidet trekant?
A: En likesidet trekant er en type af trekant, hvor alle sider er lige lange og vinklerne er på 60 grader.
Q: Hvordan beregner man arealet af en likesidet trekant?
A: Arealet af en likesidet trekant kan beregnes ved at anvende formlen halvdelen af produktet af siden og længden af højden.
Images related to the topic hvad er en ligedannet trekant
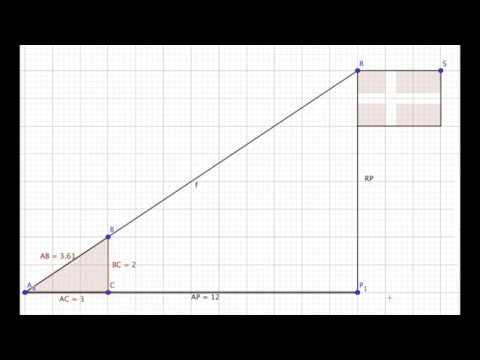
Article link: hvad er en ligedannet trekant.
Learn more about the topic hvad er en ligedannet trekant.
- Ensvinklede trekanter (Matematik C, Trigonometri)
- Ensvinklede trekanter (7.-9. klasse, Geometri) – Webmatematik
- Trekanter – Matematik, EUD/EUX, D-C – Praxis
- Introduktion til ligedannede trekanter (video) – Khan Academy
- Trekanter (7.-9. klasse, Geometri) – Webmatematik
- Ensvinklede trekanter (7.-9. klasse, Geometri) – Webmatematik
- Om ensvinklede og ligedannede trekanter
- Ligedannet trekanter – Matematik – Studieportalen.dk
- Ligedannede figurer | Skoledu.dk – Matematik i grundskolen
- Læs det – Mål
- Ligedannethed